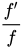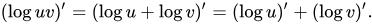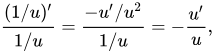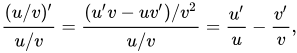Introducción a la diferenciación de funciones logaritmicas
En el ámbito de las matemáticas, específicamente en el calculo y el análisis complejo, la derivada logarítmica de una función f queda definida por la fórmula
donde f ′ es la derivada de f.
Sus descubridores fueron Leibniz y Newton.
Cuando f es una función f(x) de una variable real x, y toma valores reales, estrictamente positivos, esta es entonces la fórmula para (log f)′, o sea, la derivada del logaritmo natural de f, como se deduce aplicando directamente la regla de la cadena.
Propiedades básicas
Muchas propiedades del logaritmo real también son válidas para la derivada logarítmica, aun cuando la función no toma valores de reales positivos. Por ejemplo, dado que el logaritmo de un producto es la suma de los logaritmos de los factores, se tiene que
Por lo que para funciones reales positivas, la derivada logarítmica de un producto es la suma de la derivada logarítmica de los factores. También es posible aplicar la regla de Leibniz para la derivada del producto y así obtener 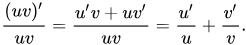
Por lo tanto, es cierto que para toda función que la derivada logarítmica de un producto es la suma de las derivadas logarítmicas de los factores (cuando las mismas están definidas).
En forma similar (de hecho es una consecuencia), la derivada logarítmica de de la función recíproca de una función es el negado de la derivada logarítmica de la función:
en la misma forma que el logaritmo de la recíproca de un número real positivo es la negación del logaritmo del número.
En forma general, la derivada logarítmica de un cociente es la diferencia de las derivadas logarítmicas del dividendo y del divisor:
en la misma forma que el logaritmo de un cociente es la diferencia de los logaritmos del dividendo y del divisor.