Diferenciación de productos de funciones
Hallar la derivada de una función aplicando la definición de derivada es un proceso largo y la mayor de las veces bastante tedioso. Afortunadamente existen varias propiedades en la derivación de funciones que los matemáticos han descubierto y establecido como teoremas. Algunos de estos teoremas son generales, aplicables a cualquier función, y otros sólo se aplican a funciones particulares. A continuación se enuncian algunos de los teoremas más importantes (se nombran enumerándolos consecutivamente para facilitar una futura referencia a ellos):
Nota: se supone, obviamente, que las funciones a las que hacen referencia los teoremas son diferenciables, esto es, que tienen derivada.
En palabras: "la derivada de una constante por una función es igual a la constante multiplicada por la derivada de la función".
Teorema D2:
En palabras: "la derivada de la suma de un número finito, n, de funciones (términos), positivas o negativas, es igual a la suma de las derivadas de cada función y con su respectivo signo".
Teorema D3:
En palabras: "la derivada del producto de dos funciones es igual a la primera función por la derivada de la segunda más la segunda función por la derivada de la primera".
Teorema D4:
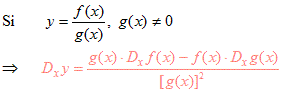
En palabras: "la derivada del cociente de dos funciones es igual a una fracción cuyo denominador es el cuadrado de la función del dividendo y cuyo numerador es la diferencia entre la función del dividendo por la derivada de la función del divisor y la función del divisor por la derivda de la función del dividendo".
Teorema D5:
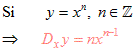
En palabras: "para hallar la derivada de la función potencia se multiplica la función por un coeficiente igual al exponente y el exponente se disminuye en la unidad ".
Teorema D6:
En palabras: "la derivada de la función constante es cero ".
Teorema D7:
En palabras: "la derivada de la función identidad es uno ".
